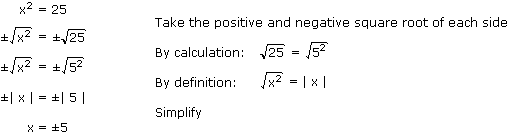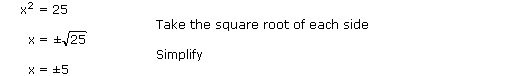Principal Square Root
Definition
Every positive number "n" has two square roots. One of them is positive (  or
or  ) , and the other is negative (
) , and the other is negative (  ). Together, these are denoted as
). Together, these are denoted as  .
.
The principal square root is the positive number square root.
Unless otherwise stated, "the square root" of a number refers ONLY to the principal square root.
Important Consequence
The square root of n2 is the absolute value of n.
This is a compact, consise way of expressing the following, (using the number 25 as an example):
Example: Square Roots (Simple Equations)
When solving a simple equation such as x2 = 25, it must be observed that there are two solutions. The two solutions to this equation are 5 and -5, since both 52 = 25 and (-5)2 = 25.
The solution above shows all of the steps.
When someone is proficient with square roots, usually only the steps shown below are written out.
Example: Square Roots (The Pythagorean Theorem)
When working with equations involving the Pythagorean Theorem, it is important to remember that the lengths of the sides of the triangle are positive numbers.
 or
or  ) , and the other is negative (
) , and the other is negative (  ). Together, these are denoted as
). Together, these are denoted as  .
.